数制从十进制到二进制，掌握数制转换的技巧

数制从十进制到二进制

数制是指用于表示数字的符号系统。在计算机科学中，最常用的数制是二进制和十进制。

十进制和二进制的区别

十进制是以 10 为基数的数制，其中使用了 10 个不同的数字 0-9。二进制是以 2 为基数的数制，其中仅使用了两个数字 0 和 1。

数制转换的技巧

将十进制数转换为二进制数需要用到除以2的方法，即反复将十进制数除以2，并记录下余数，直到商为0为止。然后将余数从下往上依次排列，就是对应的二进制数。

例如，将十进制数 27 转换为二进制数，步骤如下：

27 2 = 13 … 余 1

13 2 = 6 … 余 1

6 2 = 3 … 余 0

3 2 = 1 … 余 1

1 2 = 0 … 余 1

将余数从下往上依次排列，就得到了 27 的二进制数 11011。

二进制数的应用

二进制数在计算机科学中有着广泛的应用，主要是由于计算机只能理解0和1这两个二进制数字。通过将数字转换为二进制数，计算机可以方便地进行运算和存储数据。

结论

数制从十进制到二进制的转换方法是将十进制数反复除以2，记录下余数，然后将余数从下往上依次排列得到二进制数。二进制数在计算机科学中应用广泛。

常见问题解答

1. 二进制数有什么用途？

二进制数在计算机科学中有着广泛的应用，主要是由于计算机只能理解0和1这两个二进制数字。通过将数字转换为二进制数，计算机可以方便地进行运算和存储数据。

2. 怎样将二进制数转换为十进制数？

将二进制数转换为十进制数需要用到加权法，即将每个二进制数位上的数字与对应的权值相乘，然后将结果相加。例如，将二进制数 1011 转换为十进制数：

1 \* 2^3 + 0 \* 2^2 + 1 \* 2^1 + 1 \* 2^0 = 8 + 0 + 2 + 1 = 11

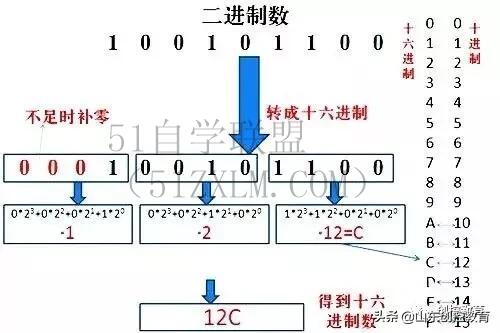
3. 什么是八进制和十六进制？

八进制是以 8 为基数的数制，其中使用了 8 个不同的数字 0-7。十六进制是以 16 为基数的数制，其中使用了 16 个不同的符号 0-9 和 A-F。在计算机科学中，八进制和十六进制数常用于表示二进制数的压缩形式。